
Gauge fixing is one of the most intriguing topics in computational electromagnetics. In this blog post, we will present an introduction and background to gauge fixing and then proceed to discuss when and how to use it in the COMSOL Multiphysics® software.
Helmholtz’s Theorem
The electromagnetics physics interfaces in COMSOL Multiphysics® are all aimed at providing solutions to Maxwell’s equations, so what is the difference between them? Why is there a need for more than one “Maxwell interface” in the first place?
To answer that question, and to deal with some common misunderstandings, let’s take a step back and look at the general, mathematical concept of a vector field, as Maxwell’s equations deal with vector fields that are functions of space and time; namely, \textbf{E}, \textbf{D}, \textbf{H}, and \textbf{B}.
A good starting point for analyzing Maxwell’s equations is Helmholtz’s theorem; also called the fundamental theorem of vector calculus. It states that any vector field \textbf{F} can be decomposed into a curl-free part and a divergence-free part. It also states that by knowing everywhere \nabla \times \textbf{F} and \nabla \cdot \textbf{F}, and for truncated domains, also knowing appropriate boundary conditions, the vector field is uniquely determined.
It may, of course, still be difficult or impossible to express \textbf{F} analytically and also nontrivial to compute it numerically.
Maxwell’s Equations
Maxwell’s equations in the differential form are written
\begin{align*}
\begin{split}
\nabla \cdot \textbf{D} = \rho, \quad \text{(Gauss’ law)} \\
\nabla \times \textbf{E} = -\frac{\partial\textbf{B}}{\partial t} , \quad
\text{(Faraday’s law)} \\
\nabla \cdot \textbf{B} = 0, \quad \text{(Magnetic Gauss’ law)} \\
\nabla \times \textbf{H} = \textbf{J} + \frac{\partial\textbf{D}}{\partial t} , \quad
\text{(Maxwell{-}Amp\`{e}re’s law)} \\
\end{split}
\end{align*}
\end{equation}
where \textbf{E} and \textbf{H} are the electric and magnetic field intensity, respectively; \textbf{D} and \textbf{B} are the electric displacement field and magnetic flux density, respectively; and \rho and \textbf{J} are the electric charge density and electric conduction current density, respectively.
In addition, material laws relate uniquely \textbf{E} to \textbf{D} and \textbf{H} to \textbf{B}. Then, from Helmholtz’s theorem, it is clear that these equations (together with sufficient boundary conditions) do provide unique vector fields \textbf{E}, \textbf{D}, \textbf{H}, and \textbf{B}, as both \nabla \times \textbf{E} and \nabla \cdot \textbf{E} are prescribed and similarly for \nabla \times \textbf{H} and \nabla \cdot \textbf{H}.
The Introduction of Potentials
It is often convenient to reformulate Maxwell’s equations in terms of scalar and vector potentials. Those are not necessarily unique and need to be analyzed using Helmholtz’s theorem, as will be discussed below.
We notice that in statics, \nabla \times \textbf{E} = \textbf{0}, and that in magnetostatics, \nabla \times \textbf{H} = \textbf{0} in the absence of currents.
This means that in those cases, we can use scalar potentials (as \nabla \times (\nabla f)= \textbf{0} for any scalar function f) to represent \textbf{E} and \textbf{H}, respectively; that is:
We also notice that \nabla \cdot \textbf{B} = 0 always holds and that \nabla \cdot \textbf{D} = 0 holds when there are no free charges.
We can then use vector potentials (\nabla \cdot (\nabla \times \textbf{F}) = 0, for any vector field \textbf{F}) to represent \textbf{B} and the divergence-free part of \textbf{D} (in absence of an electric space charge density), respectively:
Using a scalar potential is attractive in a numerical implementation as, compared to using direct representation of the field components or a vector potential, it reduces the number of unknowns by a factor 3 and the computational load (for direct solvers) up to an order of magnitude. It is also attractive from a theoretical point of view, as it is generally much easier to find analytical solutions to problems formulated using a scalar potential.
However, one of the challenges and most common sources of misunderstanding in electromagnetics is that vector calculus at the university level almost invariably starts with the special case of the analysis of curl-free fields expressed using scalar potentials. In accordance with the principle of “first impressions last”, students often forget about the more involved analysis required for fields with nonzero curl when facing real-world problems after graduating. This blog post may help to fill that gap.
On the Uniqueness of Potentials and Gauge Transformations
There are a couple of traps and pitfalls associated with the usage of potentials that have to do with the uniqueness of the potentials. As already noted, the physical fields \textbf{E}, \textbf{D}, \textbf{H}, and \textbf{B} all have unique solutions as determined by Maxwell’s equations. However, when substituting the scalar and vector potentials into Maxwell’s equations, those potentials typically have an infinite number of solutions — unless additional equations or conditions are applied.
In the following, we assume that we use the scalar electric potential V, and the magnetic vector potential \textbf{A}, together with linear relations (material laws) between \textbf{E} and \textbf{D} and between \textbf{H} and \textbf{B}, to represent the solutions to Maxwell’s equations. We are actually free to use any combination of the suggested potentials (V, V_m, \textbf{A}, and \textbf{F}) that together can represent the nonzero curls of \textbf{E} and \textbf{H}, respectively, and a nonzero divergence of \textbf{D} as required by Maxwell’s equations.
Let’s start with the scalar electric potential V. We begin in statics so that \nabla \times \textbf{E} = \textbf{0}, as there is no induced electric field in Faraday’s law. Then we can assume \textbf{E} = – \nabla V. However, V is not uniquely defined as
where C is a constant, will yield the same electrostatic field.
Thus, the scalar electric potential needs at least one additional condition fixing its general level in order to have a unique solution. Most often, this is provided as a boundary condition (ground or applied potential).
Going to the magnetic vector potential, \textbf{A}, things get more complicated as from,
one can see that we can add the gradient of any scalar function \psi to \textbf{A},
and this will yield the same (unique) \textbf{B} due to the fact that \nabla \times (\nabla \psi)= \textbf{0}.
Shifting the vector potential by a gradient of a scalar function is called a gauge transformation. Referring back to Helmholtz’s theorem, this gauge uncertainty is due to having so far only specified the curl of \textbf{A}. It is required to also specify its divergence in order to have a vector potential \textbf{A} that is unique save for adding a constant vector \textbf{C}. The latter would typically be determined by the boundary conditions. A common choice for \nabla \cdot \textbf{A} is the so-called Coulomb gauge:
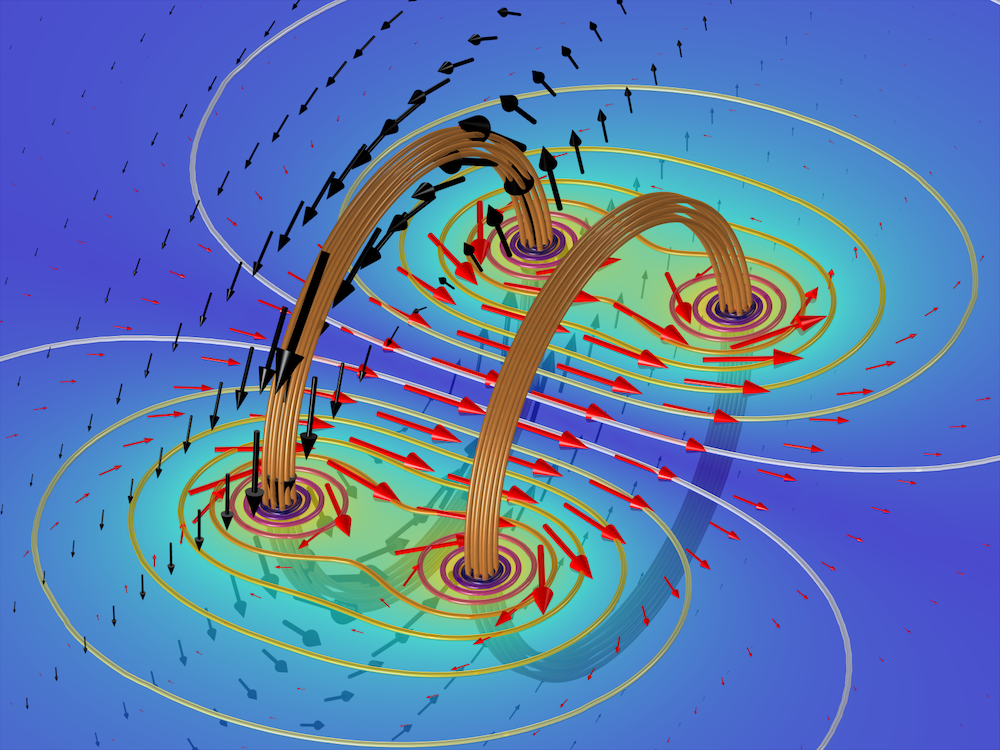
The computed \textbf{A} field (black arrows and contours for magnitude) and \textbf{B} field (red arrows and slice for magnitude) in a static Helmholtz coil. Each winding consists of 10 copper wire turns with equal current that flows parallel to the \textbf{A} field. The \textbf{A} field was computed in the Coulomb gauge \nabla \cdot \textbf{A} = 0.
Gauge Transformations in Electrodynamics
So far, we have assumed static conditions and no movement of materials so there is no induced electric field and no displacement current density. Under those conditions, electric and magnetic fields are one-way coupled. The static electric field drives a DC conduction current density that in turn generates a magnetic field.
Now, relax the condition of zero time derivatives and Faraday’s law states
and after inserting \textbf{B} = \nabla \times \textbf{A}:
Faraday’s law is fulfilled if we define:
However, repeating the gauge shifting exercise from the previous section, we see that now, in order not to change the definition of \textbf{E}, we have to shift not only \textbf{A} but also V; that is
making
Now both \textbf{A} and V depend on the choice of the gauge and both contribute to the electric field in a way that makes \textbf{E} independent of \psi.
It is also worth noting that the electric field affects the magnetic field through the conduction and displacement current density terms, \sigma\textbf{E} + \frac{\partial\textbf{D}}{\partial t}, in Maxwell–Ampère’s law in a similar way to how – \frac{\partial\textbf{B}}{\partial t} is a source term for \nabla \times \textbf{E} in Faraday’s law. Thus, dynamic electric and magnetic fields are two-way coupled (also known as fully coupled electromagnetics or “full Maxwell” formulation).
Another very important observation is that the electric potential only gives a partial, and gauge-dependent, contribution to the electric field \textbf{E}. This means that the voltage, U, can only be defined in terms of a line integral of the electric field:
Thus, the concept of using “potential difference”, which is deeply rooted in the analysis of curl-free electric fields and in circuit analysis, is not generally applicable. Further, in electrodynamics, the measured voltage is dependent upon the chosen integration path L; for example, the orientation of a pickup coil.
There are many ways of choosing the gauge. The Coulomb gauge results in an electric potential that reacts immediately to changes to the electric charge density (even far away), whereas the magnetic vector potential exhibits the effects of finite propagation speed. This may seem strange and possibly in conflict with the theory of relativity, but keep in mind that potentials are not directly measurable. Only the electric field \textbf{E} is measurable through its effect on charges, and it is, by definition, unaffected by the choice of the gauge.
The Vector Helmholtz Equation
A gauge of specific practical interest is the one where we choose \psi, such that the electric potential vanishes so that:
This gauge is only of interest for dynamic formulations, as it deteriorates in the static limit, leaving \textbf{E} undefined. It is used in the so-called vector Helmholtz equation that is used in the Frequency Domain, Electromagnetic Waves interface in the RF Module and the Frequency Domain, Magnetic Fields interface in the AC/DC Module. In the first case, the dependent variable is \textbf{E}, whereas in the second case, it is \textbf{A}. From a mathematical viewpoint, it does not make any significant difference as in the frequency domain, applying the time harmonic convention \textbf{E}(t,\textbf{r}) = Re(\textbf{E}(\textbf{r})e^{j\omega t}):
Thus \textbf{E} and \textbf{A} differ just by a global factor – j\omega.
Looking at the Magnetic Fields interface, the frequency-domain equation becomes:
At sufficiently low frequency, the terms containing omega vanish in a numerical sense and the formulation becomes identical to the magnetostatic formulation:
Then the gauge with vanishing V is effectively lost as the electric part (relating to the induced electric field \textbf{E} = – j\omega\textbf{A}) becomes numerically insignificant. Thus, the fix on \nabla \cdot \textbf{A} also becomes numerically insignificant and \textbf{A} is no longer uniquely determined.
All of this can be seen as a consequence of the electromagnetic coupling being lost in the static limit. The need for a separate equation for the electric field (based on V, which then no longer vanishes) arises.
This means that the vector Helmholtz equation is limited to situations where the induced conduction or displacement current densities are numerically significant.
The A-V Formulation
At low frequency, it is favorable to use a formulation that solves for both \textbf{A} and V, as that allows for the potentials to decouple gracefully in the static limit (having separate but coupled equations for \textbf{A} and V). The price is that you have to take explicit measures to handle the gauge uncertainty that follows; that is, to specify a condition on \nabla \cdot \textbf{A}. The Magnetic and Electric Fields interface in the AC/DC Module solves for both \textbf{A} and V.
Conclusions
So far, we have investigated the consequences of Helmholtz’s theorem when applied to Maxwell’s equations and to the usage of scalar and vector potentials to represent the physical fields \textbf{E}, \textbf{D}, \textbf{H}, and \textbf{B}. The conclusions are:
- Both the curl and divergence of a vector field must be known for it to be uniquely determined
- \textbf{E}, \textbf{D}, \textbf{H}, and \textbf{B} are uniquely determined by Maxwell’s equations plus material laws
- Introducing the scalar and vector potentials \textbf{A} and V in Maxwell’s equations is practical, but unless \nabla \cdot \textbf{A} is specified and a reference level for V is provided, the potentials are not uniquely determined
- A dynamic relation (gauge) exists between the condition on \nabla \cdot \textbf{A} and the consistent definition of V that makes the electric field \textbf{E}, independent of the chosen gauge
- The potentials \textbf{A} and V both contribute to \textbf{E}, so voltage U can only be measured as a line integral U=\int_L{\textbf{E}\cdot}d\textbf{l}, which is path dependent
- The particular gauge where V=0 leads to the vector Helmholtz equation for \textbf{A} or \textbf{E} and is useful for the modeling of electromagnetic wave propagation, induced eddy currents, and other effects with a sufficiently strong electromagnetic coupling
- However, it breaks down numerically at low frequency and then a formulation using both \textbf{A} and V is needed
In the next part of this blog series, we will talk about how to explicitly enforce a particular gauge in magnetostatics and when solving for both \textbf{A} and V in the frequency domain. We will also discuss charge conservation, that the equation of continuity is inherent in Maxwell’s equations, and how that limits the existence of solutions to cases where the source currents are solenoidal. The latter turns out to be a crucial element in successful numerical modeling in magnetostatics and low-frequency electromagnetics. Stay tuned!



Comments (2)
Iker Rodriguez
March 31, 2020Brilliant explanation, Magnus! I am eager to read the next blog on this subject!
Thomas Smith
May 15, 2020I really like your blog. It helped me a lot. Entire details were given with easy to understand words.
Showbox for pc