Steady Currents, Theory
Conservation of Currents
Conservation of currents is a fundamental law of nature and is represented in equation form as
(1)
where is the current density vector and
is the space charge density.
In the important special case of steady currents, or direct currents (DC), it holds that
(2)
Accordingly, the equation for direct currents is
(3)
This equation is mathematically similar to the equation for electrostatics in free space. Furthermore, just like the electrostatics case, Maxwell's equations imply the additional requirement that the electric field is irrotational (curl free)
(4)
which is another way of stating that in the theory of steady currents, there is no electromagnetic induction.
Materials Governed by Ohm's Law
Materials where the current density is proportional to the electric field are described by the constitutional equation known as Ohm's law
(5)
where is the electric conductivity expressed as
where denote the mobility, number density, and charge of the charge-carriers, respectively.
Then the current density can be rewritten as
where is the drift, or average, velocity of the charge-carriers.
In conductors such as copper wire, the drift velocity of the charge-carriers (electrons) is as low as a few micrometers per second, which is significantly smaller than the flow velocity of electrical energy (close to the speed of light).
In the case of an anisotropic material, the conductivity can be a 3-by-3 tensor
(6)
This implies that for certain materials, the field and the current density vector
may not be perfectly aligned.
Ohm's law is usually applied for good conductors, such as metals, where the current is primarily carried by electrons. For insulators of semiconducting materials, Ohm's law may not be adequate and more advanced models are needed.
Using the electric potential, the fundamental equation for steady currents in a material described by Ohm's law becomes
(7)
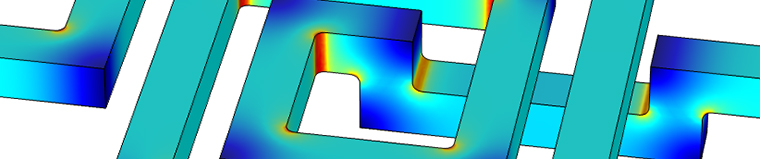
The current density in a spiral inductor where a potential difference is applied between the left and right boundaries. The picture on the left shows the current density magnitude values on the surface of the inductor. The picture on the right shows the current density magnitude values on planes cutting through the structure. Blue and red represent low and high magnitude values, respectively. In the picture on the right, the arrows show the direction of the current density. The tendency of the current to take the shortest path is visible as red areas in the inner corners of the structure.
The Steady Current Equations and Boundary Conditions at Material Interfaces
The theory for steady currents is similar to that of electrostatics. The most important equations are summarized in the following table:
| Equation Name | Differential Form | Integral Form | Boundary Condition |
|---|---|---|---|
| Current conservation | |||
| Faraday's law (steady currents) |
The meaning of Faraday's law in the theory of steady currents is identical to that of electrostatics. The meaning of the current conservation equations can be summarized in words as follows:
| Equation Name | Differential Form | Integral Form | Boundary Condition |
|---|---|---|---|
| Current conservation | Charge cannot be created or destroyed | The total current through a closed surface equals zero; this is the field equivalent of Kirchhoff's current law for electrical circuits | The normal component of the current density is continuous |
The Magnetic Field Generated by Steady Currents
The theory for steady currents described above does not reference any magnetic field. However, a magnetic field is always generated as a side effect of steady currents. Due to its stationary nature, this magnetic field does not induce any secondary currents (eddy currents), and once the steady currents are known, the magnetic field is fully determined. The magnetic field generated by steady currents can be computed, for example, from the stationary version of Maxwell–Ampère's law
Note that by taking the divergence of this equation, the conservation of currents equation is recovered in its stationary form
Power Dissipation and Resistive Loss
For a volume , the power loss in terms of field quantities is
where the power energy density is defined as
In a conductor, this power is converted to heat and referred to as resistive or ohmic loss.
Published: January 15, 2021
Last modified: January 15, 2021

