Accurate Modeling of Low-Pressure, Low-Velocity Gas Flows
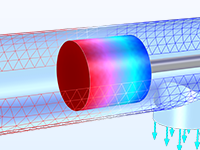
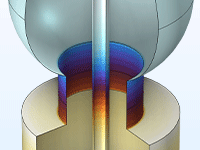
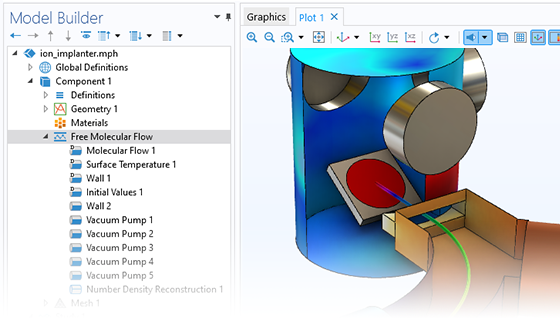
The Molecular Flow Module is ideal for the simulation of vacuum systems, including those used in semiconductor processing, particle accelerators, and mass spectrometers. Small channel applications such as shale gas exploration and flow in nanoporous materials can also be addressed.
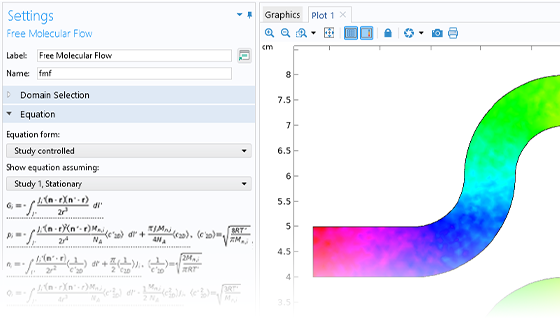
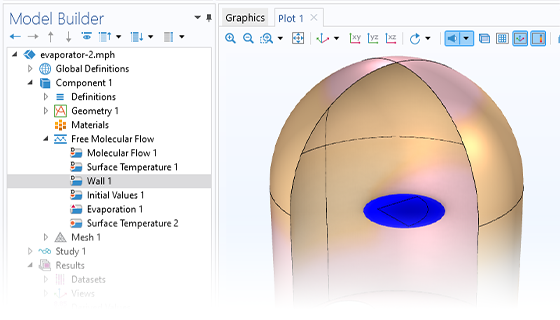
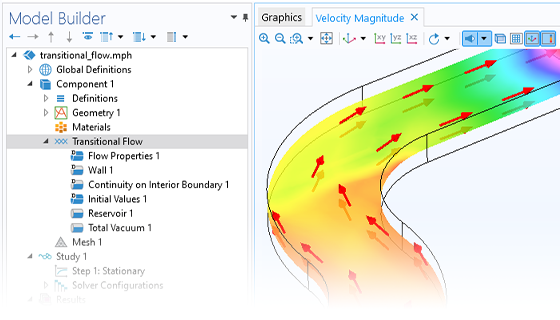
The angular coefficient method is used in the module to simulate steady-state free molecular flows, allowing for the molecular flux, pressure, and heat flux to be computed on surfaces. The number density can be reconstructed on domains, surfaces, edges, and points from the molecular flux on the surrounding surfaces. It is also possible to model isothermal and nonisothermal molecular flows and calculate the heat flux contribution from the gas molecules.