
Einzel lenses are used to focus charged particle beams in cathode ray tubes (CRTs). To properly analyze an einzel lens, we need to study the charged particles in the lens subject to appropriate electrical excitation. Here, we discuss one such example that uses the Particle Tracing Module, an add-on product to the COMSOL Multiphysics® software.
Taking a Look at Einzel Lenses
Walking into a video game tournament for the first time, I was surprised by the number of CRT televisions in the room. Why use box TVs instead of the current flat-screen versions? When I asked my brother — who had participated in these tournaments before — he told me that CRT TVs are better for displaying certain games, as they deliver the desired response time and frames per second. This advantage makes CRT TVs popular in the gaming community.

A CRT television. Image by Daniel Oines — Own work. Licensed under CC BY 2.0, via Flickr Creative Commons.
Unlike newer models, these televisions rely on CRTs, which are vacuum tubes that control how electron beams reach a screen. To focus charged particle beams, some CRTs use einzel lenses. These lenses are also found in ion propulsion systems as well as ion and electron beam experiments.
The focusing ability of an einzel lens depends on the following factors:
- Initial particle energy
- Initial beam collimation
- Voltage at each electrode
To accurately study these factors in einzel lens designs, we can use particle tracing simulation.
Particle Tracing in an Einzel Lens with COMSOL Multiphysics®
This einzel lens example consists of three cylinders aligned on the same axis. Of these cylinders, the middle one maintains a fixed voltage, while the outer two cylinders are grounded.
The electrons studied with this model have an initial kinetic energy of 20 keV. Their speed is an appreciable fraction of the speed of light. As such, relativistic effects are taken into account.
We can solve this model by using two different studies and interfaces. The first is a stationary study that uses the Electrostatics interface to calculate the electric potential and 3D electrostatic field. We then use the corresponding electric fields to exert an electric force on the modeled electrons. Second, a time-dependent study and the Charged Particle Tracing interface can be used to determine the electron particle trajectories.
In the next section, we see the results of these studies.
Simulation Results
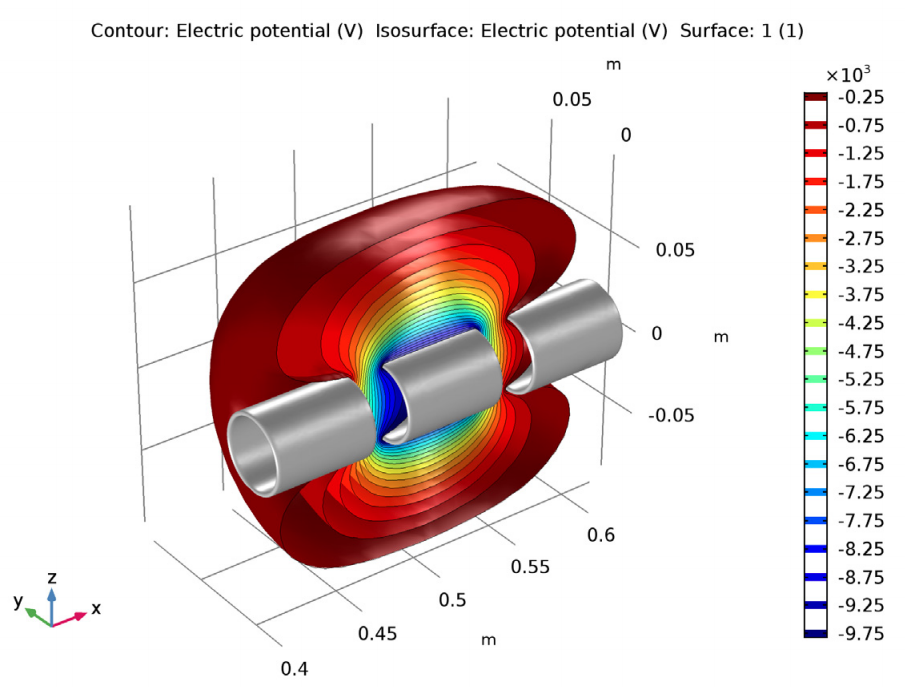
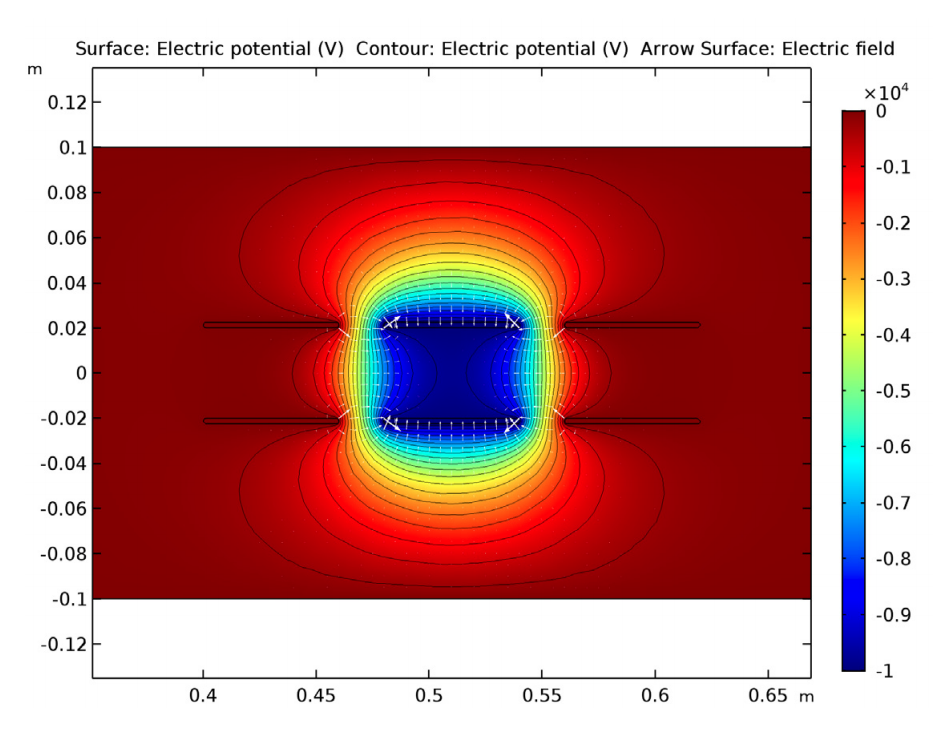
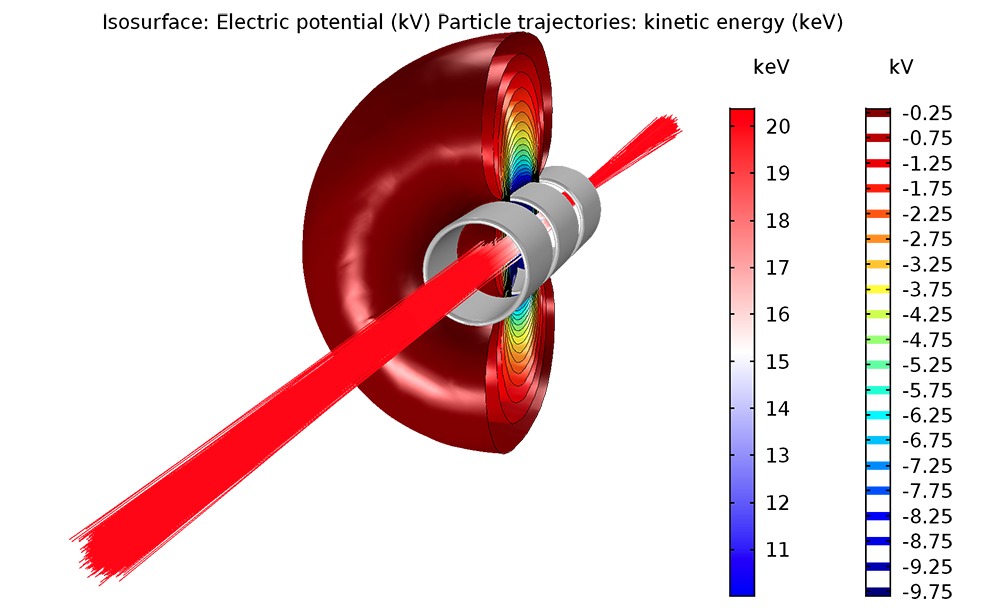
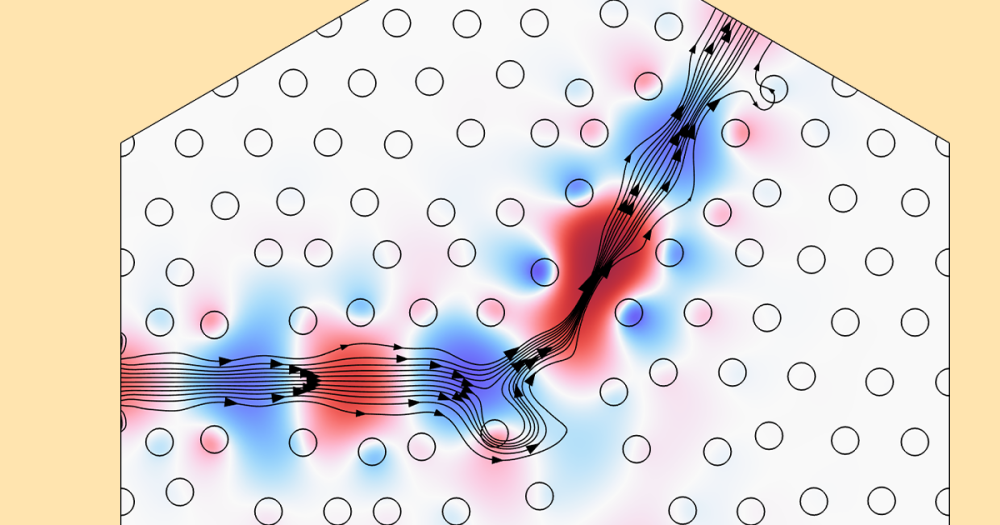
Let’s take a look at the area around the electrodes (cylinders, in this case) where the beam is focused. In the left image below, we see the equipotential surfaces that surround the electrodes. We can also study the electric potential and fringe fields by looking at a cross section near the electrodes (shown in the right image below).
The isosurfaces of the electric potential (left) and electric potential and fringe fields (right) around the electrodes.
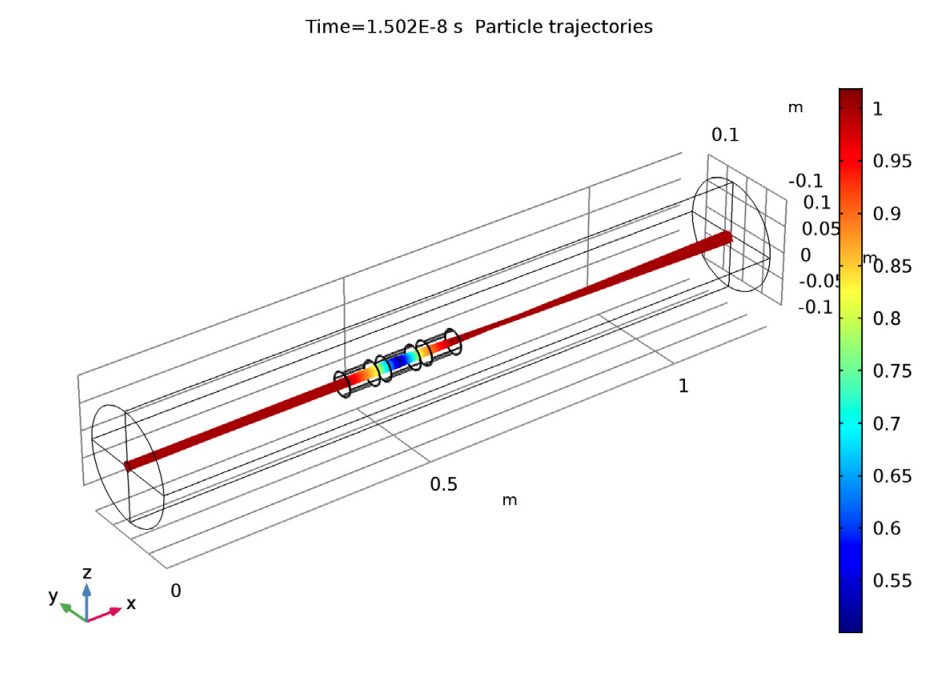
Expanding the view helps to visualize the electron trajectories through the einzel lens. As shown below, the particles reduce their speed as they approach the lens. When passing through the lens, they begin to accelerate again, eventually reaching their initial speeds.
The left image shows the electron trajectories in an einzel lens. The colors seen here represent the ratio of the particle kinetic energy to the initial kinetic energy. The right image shows the electron trajectories and the isosurfaces of the electric potential.
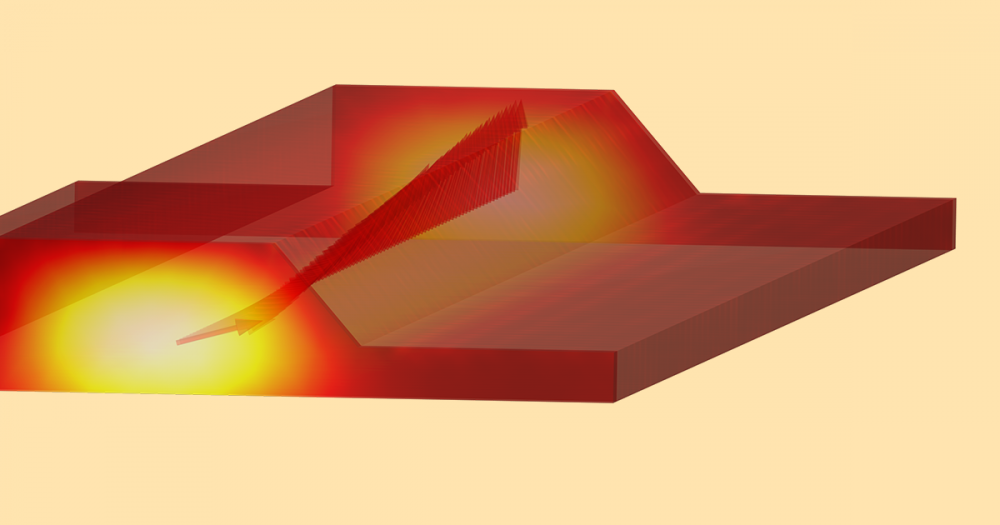
Next, we examine the nominal beam trajectory of the electrons through the einzel lens. We also account for a common measurement of the area taken up by a charged particle beam in transverse phase space: hyperemittance.
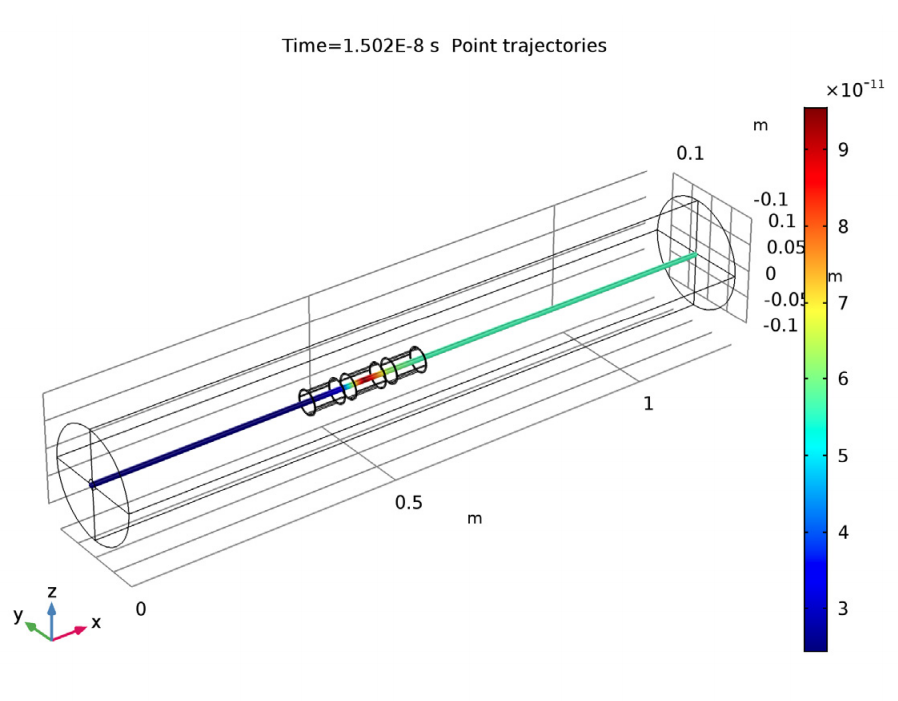
The nominal beam trajectory. Here, the color expression depicts the beam hyperemittance.
With particle tracing modeling, we are able to better analyze einzel lenses and can use these results to improve our designs. Try the einzel lens example yourself by clicking on the button below.
Further Reading
- Check out the Phase Space Distributions in Beam Physics blog series
- Learn about modeling particles in a quadrupole mass spectrometer on the COMSOL Blog
- Read this blog post on modeling particle migration in inertial focusing




Comments (0)