
When you think of beads on a string, what comes to mind? Perhaps it’s a busy street in New Orleans, Louisiana, during a Mardi Gras celebration, or making friendship bracelets at summer camp. Or, if you’re interested in studying polymers, you might think about how, when a certain force is applied to a viscoelastic fluid, the fluid starts to look like beads on a string. Let’s take a look at an example that uses an Oldroyd-B polymer.
Viscoelastic Fluids
As the name implies, viscoelastic fluids are fluids that exhibit elasticity. As a viscoelastic fluid deforms, a certain amount of force tries to get it to return to its undeformed state. Examples of this type of fluid include:
- Polymer melts
- Paints
- Suspensions of proteins

Paints are one type of viscoelastic fluid.
The Polymer Flow Module, released in 2020 with version 5.6 of the COMSOL Multiphysics® software, includes viscoelastic fluid models that you can use to account for a fluid’s elasticity and predict its exerted forces, coating uniformity, and degree of mold filling.
The following viscoelastic fluid models are included in the Polymer Flow Module:
- Oldroyd-B
- Giesekus
- FENE-P
- LPTT
Here, we will highlight the model results of a filament of Oldroyd-B fluid as it stretches due to surface tension effects. If you’d like to jump right into the step-by-step of building this model, feel free to download it here: “Beads-on-String Structure of Viscoelastic Filaments“.
Modeling Surface Tension Effects in an Oldroyd-B Polymer
Our example model starts with a long, unstretched filament of an Oldroyd-B fluid. The filament itself is modeled as a liquid cylinder with a small perturbation of its initial radius, and the flow is modeled as axisymmetric.
The Oldroyd-B fluid is modeled as a dilute solution of polymer in a Newtonian liquid. The polymer itself is characterized by two physical parameters:
- Viscosity
- Relaxation time
Since this problem is dimensionless, to simulate the dynamics of the viscoelastic filament as it thins, we turn to two dimensionless parameters:
- The Deborah number (nondimensional polymer solution relaxation time)
- The Ohnesorge number (ratio between the inertia–capillary and viscous–capillary time scales)
Modeling Results
We can determine the evolution of the viscoelastic filament at different time steps, shown below, which agrees well with existing experimental and simulation results in literature (see Reference 1 in the tutorial model documentation).

Profiles of the filament at 0, 20, 30, 100, and 300 seconds (from left to right).
The model results also show us the minimum filament radius as a function of time. What this tells us is that after the filament rapidly forms a beads-on-a-string structure, there is a slow thinning of the thread. The rate of this thinning can be determined by the balance of the surface tension effects and the elastic forces.
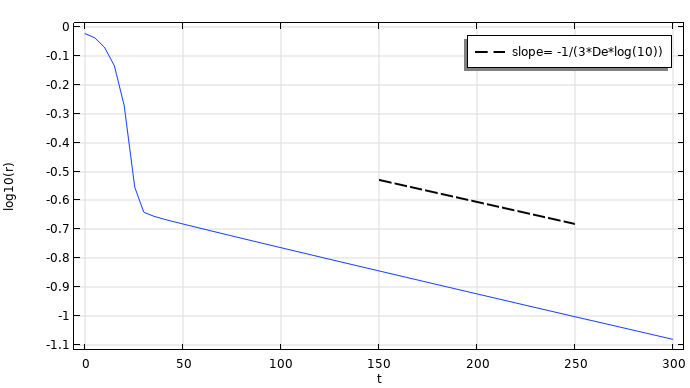
Minimum radius of the filament as a function of time.
At times much larger than the relaxation time, the viscoelastic filament consists of almost spherical drops connected by exponentially thinning threads.

We can also see that when there are particularly low viscosities or high surface tensions, satellite drops form in the beads-on-a-string structure (although you need to run the model with a finer mesh to see them).
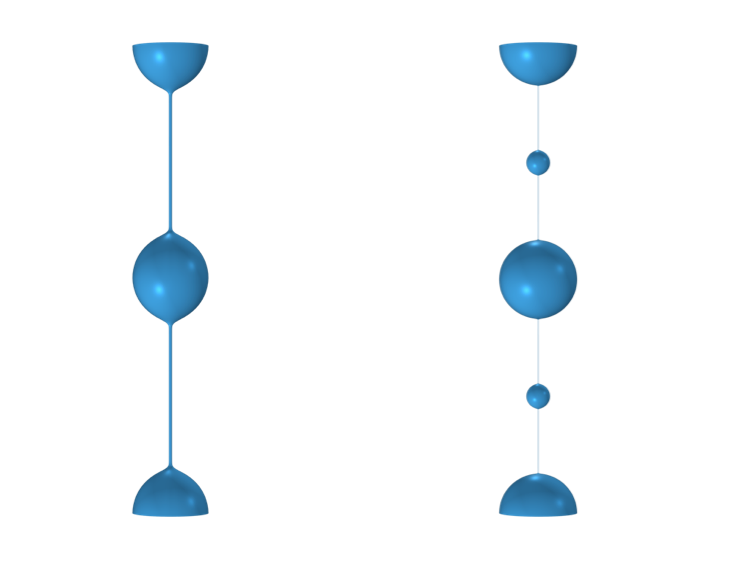
A filament of viscoelastic fluid without (left) and with (right) satellite drops.
Try It Yourself
We skipped directly to the results here, but you can learn exactly how to build the Beads-on-String Structure of Viscoelastic Filaments model by downloading the documentation and MPH-file from the Application Gallery.




Comments (0)